Answer: 0.0775
Explanation:
Given : Mean :
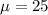
Standard deviation :
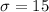
Sample size :

Since its normal distribution , then the formula to calculate the z-score is given by :-
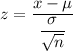
For x= 28.2 hours
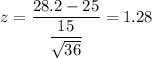
For x= 30 hours
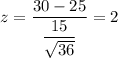
The P- value =
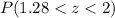

Hence, the probabiliy that the average time spent stydying for the sampe was between 28.2 and 30 hours = 0.0775