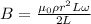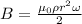Question

An infnitely long metal cylinder rotates about its symmetry axis with an angular velocity omega. The cylinder is charged. The charge density per unit volume is sigma . Find the magnetic field within the cylinder.

Answer 1

`B = (\mu_0 \rho r^2 \omega)/(2)`

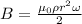
Step-by-step explanation:

Let the position of the point where magnetic field is to be determined is at distance "r" from the axis of cylinder

so here total charge lying in this region is

`q = \rho(\pi r^2 L)`

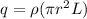
now magnetic field inside the cylinder is given as

`B = (\mu_0 N i)/(L)`

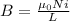
here current is given as

`i = (q\omega)/(2\pi)`

`i = (\rho (\pi r^2 L) \omega)/(2\pi)`

`i = (\rho r^2 L \omega)/(2)`

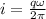
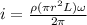
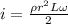
now magnetic field is given as

`B = (\mu_0 \rho r^2 L \omega)/(2L)`

`B = (\mu_0 \rho r^2 \omega)/(2)`