Question

Express the following repeating decimal as a fraction in simplest form.

0.342 repeating (line over entire decimal)

Answer 1

The fraction form of given number is
`(38)/(111)`.

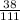Explanation:

The given repeating decimal number is

`0.\overline{342}`

Let
`x=0.\overline{342}`

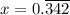
It can be written as

`x=0.342342342...`

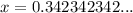
The digits repeated after 3 decimal places. So multiply both sides by 1000.

`1000x=0.342342342...* 1000`

`1000x=342.342342...`

`1000x=342+0.342342...`

`1000x=342+0.\overline{342}`

`1000x=342+x`

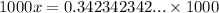
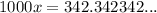
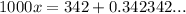
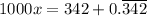
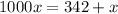
Subtract x from both the sides.

`1000x-x=342`

`999x=342`

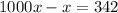
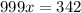
Divide both the sides by 999.

`x=(342)/(999)`

`0.\overline{342}=(342)/(999)`

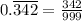
Cancel out the common factors.

`0.\overline{342}=(38)/(111)`

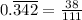
Therefore the fraction form of given number is
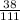`(38)/(111)`.