Question

4x^2 y+8xy'+y=x, y(1)= 9, y'(1)=25

Answer 1

Answer with explanation:

`\rightarrow 4x^2y+8x y'+y=x\\\\\rightarrow 8xy'+y(1+4x^2)=x\\\\\rightarrow y'+y*(1+4x^2)/(8x)=(1)/(8)`

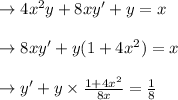
--------------------------------------------------------Dividing both sides by 8 x

This Integration is of the form ⇒y'+p y=q,which is Linear differential equation.

Integrating Factor

`=e^{\int (1+4x^2)/(8x) dx}\\\\e^{\log x^{(1)/(8)+(x^2)/(2)}\\\\=x^{(1)/(8)}* e^{(x^2)/(2)}`

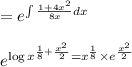
Multiplying both sides by Integrating Factor

`x^{(1)/(8)}* e^{(x^2)/(2)}* [y'+y*(1+4x^2)/(8x)]=(1)/(8)* x^{(1)/(8)}* e^{(x^2)/(2)}\\\\ \text{Integrating both sides}\\\\y* x^{(1)/(8)}* e^{(x^2)/(2)}=(1)/(8)\int {x^{(1)/(8)}* e^{(x^2)/(2)}} \, dx \\\\8y* x^{(1)/(8)}* e^{(x^2)/(2)}=\int {x^{(1)/(8)}* e^{(x^2)/(2)}} \, dx\\\\8y* x^{(1)/(8)}* e^{(x^2)/(2)}=-[x^{(9)/(8)}]*\frac{ \Gamma(0.5625, -x^2)}{(-x^2)^{(9)/(16)}}\\\\8y* x^{(1)/(8)}* e^{(x^2)/(2)}=(-1)^{(-1)/(8)}[ \Gamma(0.5625, -x^2)]+C-----(1)`

When , x=1, gives , y=9.

Evaluate the value of C and substitute in the equation 1.