Answer:
The maximum radius of the circular clock is 7 in
Explanation:
We must calculate the perimeter of the rectangle
We know that the rectangle is 10 in x 12 in
If we call L the rectangle length and we call W the width of the rectangle then the perimeter P is:

Where
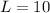
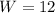
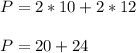
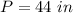
Now we know that the perimeter of a circle is:
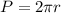
In order for the perimeter of the circumference to be equal to that of the rectangle, it must be fulfilled that:
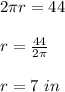
We solve the equation for r