Question

The sides and hypotenuse of a right triangle are strictly increasing with time. At the instant when x is 24 inches and y is 32 inches, dy/dt = 2 dx/dt. If dθ/dt = −0.01 radians per minute at the same instant, what is the value of dy/dt at that same instant ?

Answer 1

Explanation:

Did you perhaps mean what is the value of dx/dt at that instant? You have a value for dy/dt to be 2dx/dt. I'm going with that, so if it is an incorrect assumption I have made, I apologize!

Here's what we have:

We have a right triangle with a reference angle (unknown as of right now), side y and side x; we also have values for y and x, and the fact that dθ/dt=-.01

So the game plan here is to use the inverse tangent formula to solve for the missing angle, and then take the derivative of it to solve for dx/dt.

Here's the inverse tangent formula:

`tan\theta=(y)/(x)`

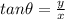
and its derivative:

`sec^2\theta(d\theta )/(dt) =(x(dy)/(dt)-y(dx)/(dt)  )/(x^2)}`

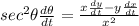
We have values for y, x, dy/dt, and dθ/dt. We only have to find the missing angle theta and solve for dx/dt.

Solving for the missing angle first:

`tan\theta =(32)/(24)`

On your calculator you will find that the inverse tangent of that ratio gives you an angle of 53.1°.

Filling in the derivative formula with everything we have:

`sec^2(53.1)(-.01)=(24(dx)/(dt)-32(dx)/(dt)  )/(24^2)`

We can simplify the left side down a bit by breaking up that secant squared like this:

`sec(53.1)sec(53.1)(-.01)`

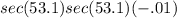
We know that the secant is the same as 1/cos, so we can make that substitution:

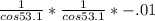`(1)/(cos53.1) *(1)/(cos53.1) *-.01` and

`(1)/(cos53.1)=1.665500191`

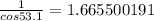
We can square that and then multiply in the -.01 so that the left side looks like this now, along with some simplification to the right:

`-.0277389=(48(dx)/(dt) -32(dx)/(dt) )/(576)`

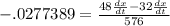
We will muliply both sides by 576 to get:

`-15.9776=48(dx)/(dt)-32(dx)/(dt)`

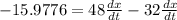
We can now factor out the dx/dt to get:

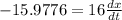`-15.9776=16(dx)/(dt)` (16 is the result of subtracting 32 from 48)

Now we divide both sides by 16 to get that

`(dx)/(dt)=-.9986(radians)/(minute)`

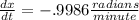
The negative sign obviously means that x is decreasing