Question

A camera is equipped with a lens with a focal length of 34 cm. When an object 2.4 m (240 cm) away is being photographed, what is the magnification?

Answer 1

The magnification is -6.05.

Step-by-step explanation:

Given that,

Focal length = 34 cm

Distance of the image =2.4 m = 240 cm

We need to calculate the distance of the object

`(1)/(u)+(1)/(v)=(1)/(f)`

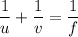
Where, u = distance of the object

v = distance of the image

f = focal length

Put the value into the formula

`(1)/(u)=(1)/(34)-(1)/(240)`

`(1)/(u)=(103)/(4080)`

`u =(4080)/(103)`

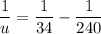
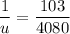
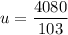
The magnification is

`m = (-v)/(u)`

`m=(-240*103)/(4080)`

`m = -6.05`

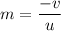
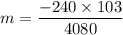
Hence, The magnification is -6.05.