Question

A record of travel along a straight path is as follows:

1. Start from rest with constant acceleration of 2.04 m/s2 for 11.0 s.
2. Maintain a constant velocity for the next 2.85 min.
3. Apply a constant negative acceleration of −9.73 m/s2 for 2.31 s.

(a) What was the total displacement for the trip?

(b) What were the average speeds for legs 1, 2, and 3 of the trip, as well as for the complete trip?

(C)COMPLETE TRIP:

Answer 1

a) Total displacement = 3986.54 m

b) Average speeds

Leg 1 -> 11.22 m/s

Leg 2 -> 22.44 m/s

Leg 3 -> 11.20 m/s

Complete trip -> 21.63 m/s

Step-by-step explanation:

a) Leg 1:

Initial velocity, u = 0 m/s

Acceleration , a = 2.04 m/s²

Time, t = 11 s

We have equation of motion s= ut + 0.5 at²

Substituting

s= ut + 0.5 at²

s = 0 x 11 + 0.5 x 2.04 x 11²

s = 123.42 m

Leg 2:

We have equation of motion v = u + at

Initial velocity, u = 0 m/s

Acceleration , a = 2.04 m/s²

Time, t = 11 s

Substituting

v = 0 + 2.04 x 11 = 22.44 m/s

We have equation of motion s= ut + 0.5 at²

Initial velocity, u = 22.44 m/s

Acceleration , a = 0 m/s²

Time, t = 2.85 min = 171 s

Substituting

s= ut + 0.5 at²

s = 22.44 x 171 + 0.5 x 0 x 171²

s = 3837.24 m

a) Leg 3:

Initial velocity, u = 22.44 m/s

Acceleration , a = -9.73 m/s²

Time, t = 2.31 s

We have equation of motion s= ut + 0.5 at²

Substituting

s= ut + 0.5 at²

s = 22.44 x 2.31 + 0.5 x -9.73 x 2.31²

s = 25.88 m

Total displacement = 123.42 + 3837.24 + 25.88 = 3986.54 m

Average speed is the ratio of distance to time.

b) Leg 1:

`v_(avg)=(123.42)/(11)=11.22m/s`

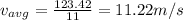
Leg 2:

`v_(avg)=(3837.24)/(171)=22.44m/s`

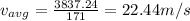
Leg 3:

`v_(avg)=(25.88)/(2.31)=11.20m/s`

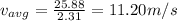
Complete trip:

`v_(avg)=(3986.54)/(11+171+2.31)=21.63m/s`