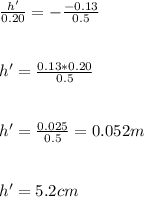Question

A 20.0 cm tall object is placed 50.0 cm in front of a convex mirror with a radius of curvature of 34.0 cm. Where will the image be located, and how tall will it be? Please show all work. Please help

Answer 1

1.Theimage will be located at -0.13m or -13 cm

2.The height of the image will be 0.052m or 5.2cm

Step-by-step explanation:

Given that;

Height of object, h=20 cm = 0.2m

Object distance in front of convex mirror, o,= 50 cm =0.5m

Radius of curvature, r, =34 cm =0.34m

Let;

Image distance, i,=?

Image height, h'=?

You know that focal length,f, is half the radius of curvature,hence

f=r/2 = 0.34/2 = 0.17m ( this length is inside the mirror, in a virtual side, thus its is negative)

f= -0.17m

Apply the relationship that involves the focal length;

`=(1)/(o) +(1)/(i) =(1)/(f)`

`=(1)/(0.5) +(1)/(i) =-(1)/(0.17)`

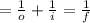
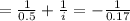
Re-arrange to get i

`(1)/(i) =-2-5.88\\\\\\(1)/(i) =-7.88\\\\i=-0.13m`

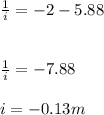
This is a virtual image formed at a negative distance produced through extension of drawing rays behind the mirror if you use rays to locate the image behind the mirror

Apply the magnification formula

magnification, m=height of image÷height of object

`m=(h')/(h) =-(i)/(o)`

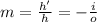
substitute the values to get the height of image h'

`(h')/(0.20) =-(-0.13)/(0.5) \\\\\\h'=(0.13*0.20)/(0.5) \\\\\\h'=(0.025)/(0.5) =0.052m\\\\\\h'=5.2cm`