Question

Are the graphs of the lines in the pair parallel? Explain.

y = 2/3x– 17
4x – 6y = –6

Answer 1

Yes they are parallel

Answer 2

Yes, they are parallel.

Explanation:

Parallel lines have the same slope. We must find the slopes of the two lines.

When the equation of a line is written in the slope-intercept form,

y = mx + b,

the slope is m.

The first line has equation

`y = (2)/(3)x - 17`

It is already written in the slope-intercept form. Comparing y = 2/3x - 17 with y = mx + b, you see that m = 2/3. The slope of the first line is 2/3.

Now we solve the second equation for y to obtain the slope-intercept form of that equation.

4x - 6y = -6

Subtract 4x from both sides.

-6y = -4x - 6

Divide both sides by -6.

`(-6)/(-6)y = (-4)/(-6)x + (-6)/(-6)`

`y = (2)/(3)x + 1`

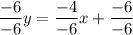
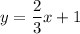
We now compare this form of the second equation with y = mx + b, and we see that m = 2/3.

Both equations have the same slope, 2/3, so the lines are parallel.