Question

Avery and Caden have saved $27,000 towards a down payment on a house. They want to keep some of the money in a bank account that pays 2.4% annual interest and the rest in a stock fund that pays 7.2% annual interest. How much should they put into each account so that they earn 6% interest per year

Answer 1

They should put $6750 in the bank account and $20,250 in the stock fund.

Explanation:

Consider the provided information that Avery and Caden have saved $27000.

Let x is the money deposit in the bank and y is the money deposit in stock fund.

Therefore,

x + y = 27000

x = 27000 - y

The bank account will pay 2.4% annual interest.

`(2.4)/(100)x+x=1.024x`

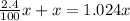
Stock fund pays 7.2% annual interest.

`(7.2)/(100)y+y=1.072y`

Therefore,

1.024 x + 1.072 y = 1.06 × 27000

Substitute the x = 27000 - y in above equation.

1.024 (27000 − y) + 1.072 y = 1.06 × 27000

27648 − 1.024 y + 1.072 y = 28620

0.048 y = 28620-27648

0.048 y = 972

y = 20250

Now, substitute the y = 20250 in x = 27000 - y.

x = 27000 − 20250

x = 6750

Hence, they should put $6750 in the bank account and $20,250 in the stock fund.