Question

Which equation is represented by the graph below?

A. y= in x-3
B. y= in x-4
C. y=e^x -3
D. y= e^x -4

Answer 1

The equation that is represented by the shown graph is the equation from the option D.

Explanation:

Answer 2

Hello!

The answer is:

The equation that is represented by the shown graph is the equation from the option D.

`y=e^(x)-4`

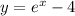
Why?

Since we are given two types of functions, exponential and logarithmic, we need to remember that there is just an option that matches with the graph.

So, from the graph we can see that we are looking for an exponential function which intercepts are located at the point (0,-3) and a point which y-coordinate is equal to 0 and its x-coordinate is located at the x-axis between the number 1 and 2.

From the given options we can see that the only exponential function that intercepts the function at y equal to -3 is the fourth option, so, let's prove that:

Option D,

`y=e^(x)-4`

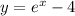
Finding the y-intercept, we need to make "x" equal to 0, so:

`y=e^(x)-4`

`y=e^(0)-4`

`y=1-4=-3`

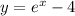
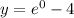
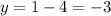
So, we know that the y-intercept point is located at (0,-3)

Finding the x-intercept, we need to make "y" equal to 0, so:

`0=e^(x)-4`

`e^(x)=4`

`ln(e^(x))=ln(4)\\x=ln(4)=1.386`

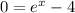
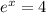
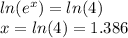
So, we know that the x-intercept point is located at (1.386,0)

Hence, we have that the axis interception points are (0,-3) and (1.386,0), so, the function that matches with the shown graph is the function from the option D.

`y=e^(x)-4`

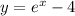
Have a nice day!

Note: I have attached a picture for better understanding.