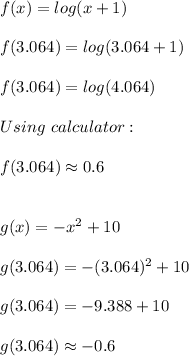Answer:
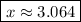
Explanation:
There is no general property that we can use to rewrite:

Then, we'll solve this problem graphically. Let's say that we have two functions:
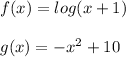
 is a logarithmic function translated one unit to the left of the pattern logarithmic function
is a logarithmic function translated one unit to the left of the pattern logarithmic function
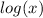 . On the other hand,
. On the other hand,
 is a parabola that opens downward and whose vertex is
is a parabola that opens downward and whose vertex is
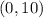 . So:
. So:
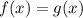
implies that we'll find the value (or values) where these two functions intersect. When graphing them, we get that this x-value is:

Then, for
 :
: