Question

Y=3x^2 + 7 + m have two intercepts ?

Answer 1

In general, quadratic equations have two x-intercepts. But sometimes it happens that a quadratic eqution has one x-intercept or no interepts. That's why we should fully analyze this equation:

Given the following equation: y=3x^2 + 7 + m

If y=0, then:

3x^2 + 7 + m = 0 ⇒ x^2 = (-m-7)/3

Then
`x =`±
`\sqrt{(-m-7)/(3)}`

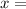Given that we can take the square root of a negative number, the only way this equation has two x-intercepts is if m<-7.

Summarizing:

The equation: y=3x^2 + 7 + m has two x-intercepts only if m is less than -7. If m equals -7, the equation has only one x-intercept, and finally, if m is greater than -7, the equation has NO x-intercepts.