Answer:
x<1.5
Explanation:
The equation is
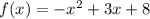
Use a graphing tool to find the vertex of the parabola.When you get the vertex from the graph, you can now write the increase as ; all x-values less than the x-value of the vertex value in the graph
From the graph, the vertex is at (1.5,10.25), the parabola opens down with maximum value y=10.25
The interval of increase is x<1.5