Question

Two parallel-plate capacitors have the same plate area, but the plate gap in capacitor 1 is twice as big as capacitor 2. If capacitance of the first capacitor is C, then capacitance of the second one is:

Answer 1

Capacitance of the second capacitor = 2C

Step-by-step explanation:

`\texttt{Capacitance, C}=(\varepsilon_0A)/(d)`

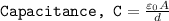
Where A is the area, d is the gap between plates and ε₀ is the dielectric constant.

Let C₁ be the capacitance of first capacitor with area A₁ and gap between plates d₁.

We have

`\texttt{Capacitance, C}_1=(\varepsilon_0A_1)/(d_1)=C`

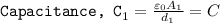
Similarly for capacitor 2

`\texttt{Capacitance, C}_2=(\varepsilon_0A_2)/(d_2)=(\varepsilon_0A_1)/((d_1)/(2))=2* (\varepsilon_0A_1)/(d_1)=2C`

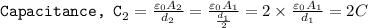
Capacitance of the second capacitor = 2C