Question

a ferris wheel with a radius of 30 feet is rotating at a rate of 2 revolutions per minute at time t=0 a chair on the ferris wheel is at the lowest point which is 10 feet above the ground which of the following models describes the height h in feet of the chair as a function of time t in seconds​

Answer 1

h=-30cos(pi/15t)+40

Answer 2

The required equation is
`f(t)=-30\cos((\pi)/(15) t)+40`.

Explanation:

The general form of cosine function is

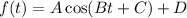`f(t)=A\cos(Bt+C)+D` .... (1)

Where, A is amplitude,
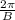`(2\pi)/(B)` is period, -C/B is phase shift and D is midline.

It is given that the radius of a ferris wheel is 30 feet. It is rotating at a rate of 2 revolutions per minute at time t=0 a chair on the ferris wheel is at the lowest point which is 10 feet above the ground.

It means the minimum value is 10 and maximum value is 10+2(30)=70.

Midline of the function is

`D=(Maximum+Minimum)/(2)=(70+10)/(2)=40`

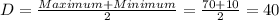
1 min = 60 seconds

Period of the function is 2.

`(2\pi)/(B)=(60)/(2)`

`(2\pi)/(B)=30`

`B=(\pi)/(15)`

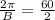
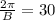
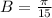
Phase shift is not given, so C=0.

Substitute
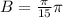`B=(\pi)/(15)\pi`, C=0 and D=40 in equation (1).

`f(t)=A\cos((\pi)/(15)i t+0)+40`

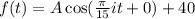
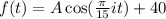`f(t)=A\cos((\pi)/(15)i t)+40` .... (2)

It is given that the graph passes through the point (0,10).

`10=A\cos(0)+40`

`10=A(1)+40`

`10-40=A`

`-30=A`

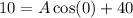
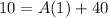
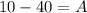
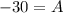
The value of A is -30. Substitute A=-30 in equation (2).

`f(t)=-30\cos((\pi)/(15) t)+40`

Therefore the required equation is
`f(t)=-30\cos((\pi)/(15) t)+40`.