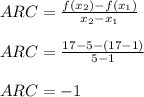Answer:
The average rate of change in f(x) over the interval [1, 5] is -1
Explanation:
Hi! Let me help you to understand this problem. Here we have the following function:
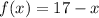
We need to compute the Average Rate of Change (ARC) in
 over the interval
over the interval
![[1, 5]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3gw4t1pqwzfbiqkqhzryoowruwkgcezo5b.png) . So what is the average rate of change of a function? In general, for a nonlinear graph whose slope changes at each point, the average rate of change between any two points
. So what is the average rate of change of a function? In general, for a nonlinear graph whose slope changes at each point, the average rate of change between any two points
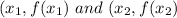 is defined as the slope of that line through that two points. Here we have a linear function, so the average rate of change will be the slope of the line:
is defined as the slope of that line through that two points. Here we have a linear function, so the average rate of change will be the slope of the line:
So:
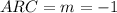
This can also be calculated as: