Question

Two forces of magnitudes 4.0 Newtons and 3.0 Newtons pull on a box. The forces make an angle of 40° with each other. What is the magnitude of a third force that must be applied to keep the box in equilibrium?

Answer 1

6.6 N

Step-by-step explanation:

Let's take the direction of the force of 4.0 N as positive x-direction. This means that the force of 3.0 N is at 40 degrees above it. So the components of the two forces along the x- and y-directions are:

`F_(1x) = 4.0 N\\F_(1y) = 0`

`F_(2x) = 3.0 N cos 40^(\circ)=2.3 N\\F_(2y) = 3.0 N sin 40^(\circ) = 1.9 N`

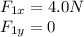
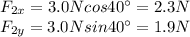
So the resultant has components

`F_x = F_(1x)+F_(2x)=4.0 N +2.3 N = 6.3 N\\F_y = F_(1y) + F_(2y) = 0 + 1.9 N = 1.9 N`

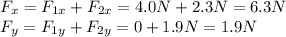
So the magnitude of the resultant is

`F=√(F_x^2 +F_y^2)=√((6.3)^2+(1.9)^2)=6.6 N`

And in order for the body to be balanced, the third force must be equal and opposite (in direction) to this force: so, the magnitude of the third force must be 6.6 N.