Question

Consider the following reaction at a high temperature. Br2(g) ⇆ 2Br(g) When 1.35 moles of Br2 are put in a 0.780−L flask, 3.60 percent of the Br2 undergoes dissociation. Calculate the equilibrium constant Kc for the reaction.

Answer 1

Answer : The equilibrium constant
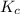`K_c` for the reaction is, 0.1133

Explanation :

First we have to calculate the concentration of
`Br_2`.

`\text{Concentration of }Br_2=\frac{\text{Moles of }Br_2}{\text{Volume of solution}}`

`\text{Concentration of }Br_2=(1.35moles)/(0.780L)=1.731M`

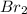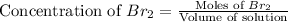
Now we have to calculate the dissociated concentration of
`Br_2`.

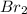The balanced equilibrium reaction is,

`Br_2(g)\rightleftharpoons 2Br(aq)`

Initial conc. 1.731 M 0

At eqm. conc. (1.731-x) (2x) M

As we are given,

The percent of dissociation of
`Br_2` =
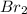`\alpha` = 1.2 %

So, the dissociate concentration of
`Br_2` =
`C\alpha=1.731M* (1.2)/(100)=0.2077M`

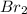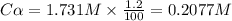
The value of x = 0.2077 M

Now we have to calculate the concentration of
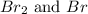`Br_2\text{ and }Br` at equilibrium.

Concentration of
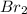`Br_2` = 1.731 - x = 1.731 - 0.2077 = 1.5233 M

Concentration of
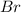`Br` = 2x = 2 × 0.2077 = 0.4154 M

Now we have to calculate the equilibrium constant for the reaction.

The expression of equilibrium constant for the reaction will be :

`K_c=([Br]^2)/([Br_2])`

Now put all the values in this expression, we get :

`K_c=((0.4154)^2)/(1.5233)=0.1133`

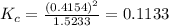
Therefore, the equilibrium constant
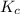`K_c` for the reaction is, 0.1133