Answer:
Option B
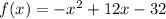
Explanation:
we know that
For the given values, the quadratic function is a vertical parabola open downward (vertex is a maximum)
The equation in vertex form is equal to
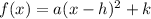
where
(h,k) is the vertex
a is a coefficient
we have
(h,k)=(6,4)
so
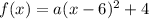
Find the value of a
For x=8, y=0 -----> the y-intercept
substitute
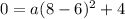
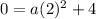
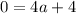

substitute
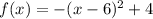
Convert to standard form
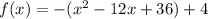
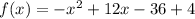
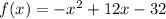
The graph in the attached figure