Answer:
- 4(x -1); 1
- 20 +2.5(x -6); 6
Explanation:
A piecewise function has different function descriptions on different domains.
Domains
The description of the rate schedule tells you the rates are different for ...
- the first hour
- hours after the first, up to 6 hours
- hours after the 6th
These descriptions of the intervals for which charges are different will help you fill in the domain descriptions on the right side of the table.
The description for the first hour is already filled in for you:
0 < x ≤ 1
The description "the second to sixth hour" refers to time periods after 1 hour, but not greater than 6 hours:
1 < x ≤ 6
The description "after 6 hours" is represented by ...
x > 6
Note that the inequality symbols are chosen so that the function is defined for all values of x. That is, the end of one interval adjoins, but does not overlap, the start of the next interval. (Actually, this function is undefined for x ≤ 0.)
Function formulas
Second to sixth hour
The wording "$4 per hour" is described by ...
4h
where h is the number of hours after the first. That is, ...
h = x -1
So, the parking charge after the first hour, up until the sixth hour, is ...
4(x -1) . . . . charge for 1 < x ≤ 6
After six hours
The wording "$2.50 per hour" is described by ...
2.50h
where h is the number of hours after six. That is, ...
h = x -6
So, the parking charge for hours after the sixth is ...
2.50(x -6)
However, there is also a charge for the hours up to the 6th. That charge is added to this one for hours after the 6th. From above, we know that the charge for parking 6 hours is ...
4(6 -1) = 20 . . . . dollars
Added to the charge for hours after the 6th, we find the total parking charge to be ...
20 +2.50(x -6) . . . . . . charge for x > 6
If you like, this can be simplified to ...
2.5x +5 . . . . . for x > 6
Summary
The entire function can be described by the simplified form ...
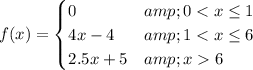
__
Additional comment
Piecewise functions are often used for tables of charges. In general, we like to see the function be continuous: its graph can be drawn without lifting the pencil, as here.
However, sometimes there is an extra charge for quantities above a certain value (as for utility use).
Sometimes, there is an extra discount for production above a certain level (possibly due to changes in transportation or tooling costs). Ordering n+1 may cost less than ordering n in those cases.