Answer:
D. y - 5 =3(x + 1)
Explanation:
Given equation of line:
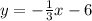
Comparing it with the standard form of equation of line
y=mx+b
m = -1/3
Let m1 be the slope of line perpendicular to the given line.
We know that the product of slopes of two perpendicular lines is -1.

The equation of line in point slope form is:

where x_1 and y_1 is the point from which the line passes.
So, putting the values of slope and point,
![y-5 = 3[x-(-1)]\\y-5=3(x+1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/fsllpy4hdjerixhl45lfipm3n48oy2ps76.png)
Option D is correct ..