Answer:
Shown below
Explanation:
To solve this problem, we need to analyze the leading coefficient and the roots of the polynomial function:
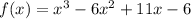
Recall that a polynomial function can be represented by:
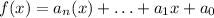
So the leading coefficient is
 . In our problem, this coefficient is
. In our problem, this coefficient is
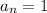
Since
 is odd and the leading coefficient
is odd and the leading coefficient
 , then the graph must falls to the left and rise to the right. Also, the roots are
, then the graph must falls to the left and rise to the right. Also, the roots are
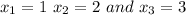 . So the only graph that matches this is the fourth one as indicated below.
. So the only graph that matches this is the fourth one as indicated below.