Question

55 L of a gas at 25oC has its temperature increased to 35oC. What is its new volume?

Answer 1

Approximately 56.8 liters.

Assumption: this gas is an ideal gas, and this change in temperature is an isobaric process.

Step-by-step explanation:

Assume that the gas here acts like an ideal gas. Assume that this process is isobaric (in other words, pressure on the gas stays the same.) By Charles's Law, the volume of an ideal gas is proportional to its absolute temperature when its pressure is constant. In other words

`\displaystyle V_2 = V_1\cdot (T_2)/(T_1)`,

where

• 
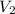  `V_2` is the final volume,
• 
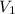  `V_1` is the initial volume,
• 
  `T_2` is the final temperature in degrees Kelvins.
• 
  `T_1` is the initial temperature in degrees Kelvins.

Convert the temperatures to degrees Kelvins:

`T_1 = \rm 25^(\circ)C = (25 + 273.15)\; K = 298.15\; K`.

`T_2 = \rm 35^(\circ)C = (35 + 273.15)\; K = 308.15\; K`.

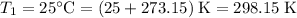Apply Charles's Law to find the new volume of this gas:

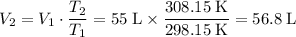`\displaystyle V_2 = V_1\cdot (T_2)/(T_1) = \rm 55\;L * (308.15\; K)/(298.15\; K) = 56.8\; L`.