Question

In a survey, 11 people were asked how much they spent on their child's last birthday gift. The results were roughly bell-shaped with a mean of $46 and standard deviation of $14. Construct a confidence interval at a 90% confidence level.

Answer 1

The population standard deviation is not known.

90% Confidence interval by T₁₀-distribution: (38.3, 53.7).

Explanation:

The "standard deviation" of $14 comes from a survey. In other words, the true population standard deviation is not known, and the $14 here is an estimate. Thus, find the confidence interval with the Student t-distribution. The sample size is 11. The degree of freedom is thus
`11 - 1 = 10`.

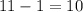Start by finding 1/2 the width of this confidence interval. The confidence level of this interval is 90%. In other words, the area under the bell curve within this interval is 0.90. However, this curve is symmetric. As a result,

• The area to the left of the lower end of the interval shall be
  `1/2 \cdot (1 - 0.90)= 0.05`.
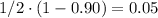• The area to the left of the upper end of the interval shall be
  `0.05 + 0.90 = 0.95`.

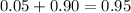Look up the t-score of the upper end on an inverse t-table. Focus on the entry with

• a degree of freedom of 10, and
• a cumulative probability of 0.95.

`t \approx 1.812`.

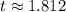This value can also be found with technology.

The formula for 1/2 the width of a confidence interval where standard deviation is unknown (only an estimate) is:

`\displaystyle t \cdot (s_(n-1))/(√(n))`,

where

• 
  `t` is the t-score at the upper end of the interval,
• 
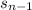  `s_(n-1)` is the unbiased estimate for the standard deviation, and
• 
  `n` is the sample size.

For this confidence interval:

• 
  `t \approx 1.812`,
• 
  `s_(n-1) = 14`, and
• 
  `n = 11`.

Hence the width of the 90% confidence interval is

`\displaystyle 1.812 * (14)/(√(10)) \approx 7.65`.

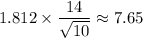The confidence interval is centered at the unbiased estimate of the population mean. The 90% confidence interval will be approximately:

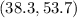`(38.3, 53.7)`.