Question

Alexis put $2000 in savings account. After 4 years, she had $2543 in the account. What rate of interest did she earn?

Answer 1

A

Explanation:

Hihi. So, this is a nice application of interest rates as well as properties of exponentials/logarithms. As you know, the basic equation for interest rates is A= Pe^(rt) where A is your final amount, P is your initial, r is your rate of interest, and t is the time the money was accumulating interest. After cleaning up, you get in a situation due to you having e still lying around. Luckily, if you take the natural log of e, all you have left behind is the previous exponent. Thus, you can take the natural log of both sides, divide by 4, and then simplify to see that your final interest rate is ~6%

Answer 2

A. 6%

Explanation:

Since, the given amount formula is,

`A=Pe^(rt)`

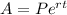
Where, P is the initial amount,

r is the periodic rate of interest,

t is the number of periods,

Here, P = $ 2000,

t = 4 years,

A = $ 2543,

By substituting the values,

`2543=2000e^(4r)`

`1.2715=e^(4r)`

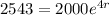
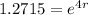
Taking ln on both sides,

`ln(1.2715)=4r`

`\implies r = 0.06004932647\approx 0.06 = 6\%`

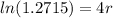
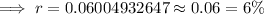
Hence, the rate of interest is 6 %.

Option 'A' is correct.