Question

A takes 3 hours more than B to walk 30 km. But if A doubles his pace, he is ahead of B by 3/2 hours . Find their speed of walking.​

Answer 1

Initial speed:

• A:
  `\displaystyle \rm (10)/(3)\; km/ h`.
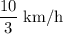• B:
  `\rm 5\; km/ h`.

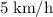Explanation:

Both equations are concerned about the time differences between A and B. To avoid unknowns in the denominators,

• let
  `x` be the initial time in hours for A to walk 30 km, and
• let
  `y` be the time in hours for B to walk 30 km.

First equation:

"A takes 3 hours more than B to walk 30 km."

`x = y + 3`.

`x - y = 3`.

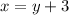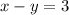When A doubles his pace, he takes only 1/2 the initial time to cover the same distance. In other words, now it takes only
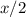`x/2` hours for A to walk 30 km.

Second equation:

"[A] is ahead of B by 3/2 hours [on their 30-km walk.]"

`\displaystyle (x)/(2) + (3)/(2) = y`.

`\displaystyle (1)/(2)x - y = -(3)/(2)`.

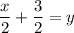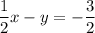Hence the two-by-two linear system:

`\left\{\begin{aligned}&x - y = 3\\&(1)/(2)x - y = -(3)/(2)\end{aligned}\right.`.

Solve this system for
`x` and
`y`:

Subtract the second equation from the first:

`\displaystyle (1)/(2)x = (9)/(2)`.

`x = 9`.

`y = 6`.

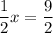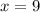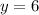It initially takes 9 hours for A to walk 30 kilometers. The initial speed of A will thus be:

`\displaystyle v = (s)/(t) = \rm (30\; km)/(9\; h) = (10)/(3)\; km/h`.

It takes 6 hours for B to walk 30 kilometers. The speed of B will thus be:

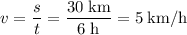`\displaystyle v = (s)/(t) = \rm (30\; km)/(6\; h) = 5\; km/h`.