Question

A damaged 1200-kg car is being towed by a truck. Neglecting the friction, air drag, and rolling resistance, determine the extra power required (a) for constant velocity on a level road, (b) for constant velocity of 50 km/h on a 30° (from horizontal) uphill road, and (c) to accelerate on a level road from stop to 90 km/h in 12 s.

Answer 1

(a) 0 W

In this situation, the car is moving on a level road at constant velocity. This means that its acceleration is zero:

a = 0

But this also means that the net force acting on the car is zero, according to Newton's second law:

F = ma = 0

The power required to move the car is

P = Fv

where F is the force applied to the car and v the velocity. Since there are no air drag/frictional forces, the force applied to the car is exactly zero: so, the extra power needed to keep the car in motion at constant velocity is also zero.

(b) 81815 W

In this situation, the car is moving on an uphill road, so there is a component of the weight parallel to the incline acting agains the direction of motion of the car. This component of the weight is given by

`W=mg sin \theta`

where

m = 1200 kg is the mass of the car

g = 9.81 m/s^2 is the acceleration of gravity

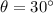`\theta = 30^(\circ)` is the angle of the incline

Substituting,

`W=(1200 kg)(9.81 m/s^2)(sin 30^(\circ) )=5886 N`

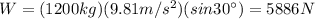
So the truck must exerts an additional force of F = 5886 N to keep the car in motion at constant velocity.

The velocity of the car is

v = 50 km/h = 13.9 m/s

So the extra power needed is

P = Fv = (5886 N)(13.9 m/s) = 81,815 W

(c) 31250 W

Here the car accelerates to a final velocity of

v = 90 km/h = 25 m/s

from an initial velocity of

u = 0

So the work done on the car is equal to its change in kinetic energy, so:

`W=K_f - K_i = (1)/(2)mv^2 - (1)/(2)mu^2 = (1)/(2)(1200 kg)(25 m/s)^2 -0 =3.75\cdot 10^5 J`

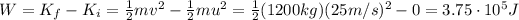
The extra power erogated by the truck therefore must be

`P=(W)/(t)`

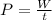
where

t = 12 s

is the time taken

Substituting,

`P=(3.75\cdot 10^5 J)/(12 s)=31250 W`