Question

There are 20 multiple-choice questions on an exam, each having responses a, b, c, or d. Each question is worth 5 points, and only one response per question is correct. Suppose a student guesses the answer to each question, and her guesses from question to question are independent. If the student needs at least 40 points to pass the test, the probability the student passes is closest to

Answer 1

Ok, the student needs 40 points and each question is worth 5, so 40/5 = 8 questions are needed.

Each question has 4 possibilities, 1 is right, so the chances to guess it correctly is one in 4, or 1/4, or 25%.

`(8)/(20) = (2)/(5)`

To know the probability to pass the exam we can do:

`(25)/(100)*(2)/(5) = 10%`

Answer 2

Answer: 0.102 or 10.2%.

Explanation:

Given : Number of multiple-choice questions = 20

Number of options in any question=4

Each question is worth 5 points and only one response per question is correct.

Probability of getting a correct answer =
`(1)/(4)=0.25`

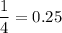
If the student needs at least 40 points to pass the test, that mean he needs at-least
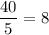`(40)/(5)=8` questions correct.

Let x denotes the number of correct questions .

By using binomial distribution , we find

`P(x\geq8)=1-P(x<8)\\\\ =1-P(x\leq7)\\\\=1-0.898\ \ \text{[By using binomial table for n= 20 , p=0.25 and x=7]}\\\\=0.102`

[Binomial table gives the probability
`P(X\leq x)=\sum_(x=0)^c^nC_xp^x(1-p)^(n-x)` ]

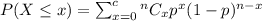Hence, the probability the student passes is closest to 0.102 or 10.2%.