Question

The mean length of six-year-old rainbow trout in the Arolik River in Alaska is 481 millimeters with a standard deviation of 41 millimeters. Assume these lengths are normally distributed. What proportion of six-year-old rainbow trout are less than 501 millimeters long?

Answer 1

Answer: 0.688

Explanation:

Given: Mean :
`\mu = 481 \text{ millimeters}`

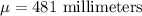
Standard deviation :
`\sigma=871\text{ millimeters}`

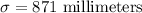
Sample size :
`n=1600`

We assume these lengths are normally distributed.

Then the formula to calculate the z score is given by :-

`z=(X-\mu)/(\sigma)`

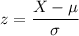
For X=501

`z=(501-481 )/(41)=0.487804878049\approx0.49`

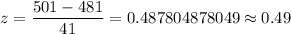
The p-value of z =
`P(z<0.49)=0.6879331\approx0.688`

Now, the probability of the newborns weighed between 1492 grams and 4976 grams is given by :-

Hence, The proportion of six-year-old rainbow trout are less than 501 millimeters long = 0.688