Question

Solve the inequality and complete a line graph representing the solution. In a minimum of two sentences, describe the solution and the line graph.

8 3x + 5

Answer 1

The solution is
`x\leq 1`

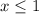
All real numbers less than or equal to 1

The graph in the attached figure

Explanation:

we have

`8\geq 3x+5`

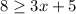
Subtract 5 both sides

`8-5\geq 3x`

`3\geq 3x`

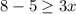
Divide by 3 both sides

`1\geq x`

Rewrite

`x\leq 1`

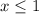
The solution is the interval ------> (-∞,1]

All real numbers less than or equal to 1

In a number line the solution is the shaded area at left of x=1 (close circle)

see the attached figure