Question

an energy plant is looking into putting in a system to remove harmful pollutants from its emissions going into Earth's atmosphere. The cost of removing the pollutants can be modeled using the function C = 25000P/100 -P what is the vertical asymptote?

Answer 1

The vertical asymptote is at P = 100

Explanation:

* Lets explain what are the vertical asymptotes

- Vertical asymptotes are vertical lines which correspond to the zeroes

of the denominator of a rational function

- Vertical asymptotes can be found by solving the equation n(x) = 0

where n(x) is the denominator of the function t(x)/n(x)

- Note: this only applies if the numerator t(x) is not equal zero for the

same value of x

# Example: to find the vertical asymptote to
`f(x)=(3x-1)/(x-5)`

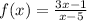
put the denominator x - 5 = 0, and solve it

the value of x = 5, then the vertical asymptote is at x = 5

* Lets solve the problem

- The equation of the cost is
`C=(25000P)/(100-P)`

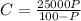
∵ The denominator of C is (100 - P)

- To find the vertical asymptote equate the denominator by zero

∴ 100 - P = 0 ⇒ add P for both sides

∴ P = 100

∴ There is a vertical asymptote at P = 100

* The vertical asymptote is at P = 100