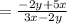Question

(Please Hurry!) Which expression is equivalent to the following complex fraction?

Answer 1

The expression equivalent to the given complex fraction is

`(-2x+5y)/(3x-2y)`

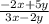
Explanation:

An easy way to solve the complex fraction is to solve the numerator and denominator separately.

Numerator:

`(-2)/(x) + (5)/(y)\\ = (-2y + 5x)/(xy)`

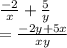
Denominator:

`(3)/(y) + (-2)/(x)\\ = (3x - 2y)/(xy)`

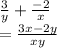
Solving the complex fraction:

`[(-2)/(x) + (5)/(y)] / [(3)/(y) + (-2)/(x)]\\= [(-2y + 5x)/(xy)] / [(3x - 2y)/(xy)]`

`=(-2y + 5x)/(xy) * (xy)/(3x - 2y)`

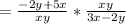
Common terms in the numerator and denominator cancels each other(Cross multiplication) :

`= (-2y + 5x)/(3x - 2y)`