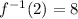Answer:
The value of
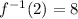
Explanation:
* Lets revise how to find the inverse function
- At first write the function as y = f(x)
- Then switch x and y
- Then solve for y
- The domain of f(x) will be the range of f^-1(x)
- The range of f(x) will be the domain of f^-1(x)
* Now lets solve the problem
- The inverse of the logarithmic function is an exponential function
∵
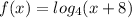
- Write the function as y = f(x)
∴
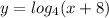
- Switch x and y
∴
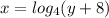
- Lets solve it to find y
# Remember:
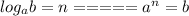
- Use this rule to find y
∴
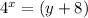
- Subtract 8 from both sides
∴
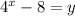
∴
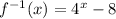
- Lets substitute x by 2
∴
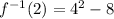
- The value of 4² = 16
∴
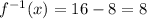
* The value of