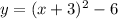Answer:
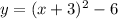
Explanation:
The equation of a parabola in Vertex form is:

Where
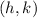 is the vertex of the parabola
is the vertex of the parabola
We can rewrite the function
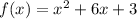 as:
as:
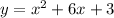
In order to convert it into vertex form we need to Complete the square:
Take the coefficient of the x term, divide it by 2 and square it:
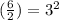
Add and subtract 3² on the right side:
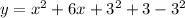
Now we must convert the right side to a squared expression, then we get: