Question

An airplane flying parallel to the ground undergoes two consecutive displacements. The first is 76 km at 39.8◦ west of north, and the second is 156 km at 59.9◦ east of north. What is the magnitude of the plane’s total displacement? Answer in units of km. 020 (part 2 of 2) 10.0

Answer 1

Magnitude of total displacement = 162.87 km

Step-by-step explanation:

Let east be x axis and north be y axis.

The first is 76 km at 39.8◦ west of north.

Displacement 1 = 76 km at 39.8◦ west of north = 76 km at 129.8◦ north of east.

Displacement 1 = 76 cos129.8 i + 76 sin 129.8 j = -48.65 i + 58.39 j

The second is 156 km at 59.9◦ east of north.

Displacement 2 = 156 km at 59.9◦ east of north = 156 km at 31.1◦ north of east.

Displacement 2 = 156 cos31.1 i + 156 sin 31.1 j = 133.58 i + 80.58 j

Total displacement = Displacement 1 + Displacement 2

Total displacement = -48.65 i + 58.39 j + 133.58 i + 80.58 j = 84.93 i + 138.97 j

`\texttt{Magnitude of total displacement =}√(84.93^2+138.97^2)=162.87km`

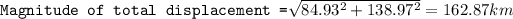
Magnitude of total displacement = 162.87 km

Answer 2

162 km

Step-by-step explanation:

A diagram can be helpful.

Using the law of cosines, we can find the magnitude of the distance (c) to satisfy ...

c^2 = a^2 +b^2 -2ab·cos(C)

where C is the internal angle of the triangle of vectors and resultant. Its value is ...

180° -39.8° -59.9° = 80.3°

Filling in a=76 and b=156, we get ...

c^2 = 76^2 +156^2 -2·76·156·cos(80.3°) ≈ 26116.78

c ≈ √26116.78 ≈ 161.607

The magnitude of the total displacement is about 162 km.

_____

Please note that in the attached diagram North is to the right and East is up. That alteration of directions does not change the angles or the magnitude of the result.