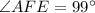Answer:
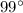
Explanation:
In the given picture , we have a hexagon having all its exterior angles.
We know that the sum of all exterior angles is
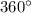 .
.
Let x be measure of
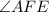
Then , the exterior angle to
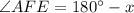
Then According to the given figure , we have
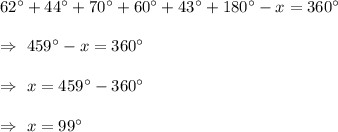
Hence, the measure of