2 Answers

Barakadam · Answer 1 · 2020-02-04T21:53:41+0000

Answer:

144.5cm^2

Explanation:

First find area of the rectangle

Area of a rectangle = L*B

= 9*13 = 117cm^2

Now find area of the triangle

Area of triangle. = 1/2 base * height

Height = 13 - 8 =5cm

Area of the triangle = 1/2 *11 *5 = 27.4

Now area of the who figure is area of rectangle + area of triangle

= 117 + 27.5

= 144.5cm^2

Fantini · Answer 2 · 2020-02-08T18:11:04+0000

For this case we have that the area of the figure is given by the area of a rectangle plus the area of a triangle.

The area of a rectangle is given by:

A = a * b

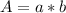
Where a and b are the sides of the rectangle.

According to the figure we have:

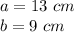
$a = 13 \ cm\\b = 9 \ cm$

So, the area of the rectangle is:

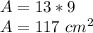
$A = 13 * 9\\A = 117 \ cm ^ 2$

On the other hand, the area of a triangle is given by:

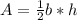
$A = \frac {1} {2} b * h$

Where b is the base of the triangle and h the height. According to the figure we have:

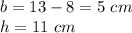
$b = 13-8 = 5 \ cm\\h = 11 \ cm$

Substituting:

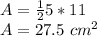
$A = \frac {1} {2} 5 * 11\\A = 27.5 \ cm ^ 2$

Adding up we have the total area is:

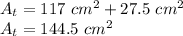
$A_ {t} = 117 \ cm ^ 2 + 27.5 \ cm ^ 2\\A_ {t} = 144.5 \ cm ^ 2$

Answer:

Option B

Please log in or register to add a comment.