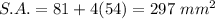2 Answers

Matt Robertson · Answer 1 · 2020-01-29T18:12:31+0000

Answer:

S.A. = 297 mm²

Explanation:

We have a square in the base and four triangles on the lateral surface.

The formula of an area of a square:

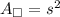
$A_(\square)=s^2$

s - side

We have s = 9mm. Susbtitute:

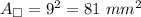
$A_(\square)=9^2=81\ mm^2$

The formula of an area of a triangle:

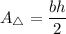
$A_(\triangle)=(bh)/(2)$

b - base

h - height

We have b = 9 mm and h = 12 mm. Substitute:

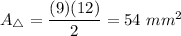
$A_(\triangle)=((9)(12))/(2)=54\ mm^2$

The Surface Area:

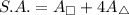
$S.A.=A_(\square)+4A_(\triangle)$

Substitute:

$S.A.=81+4(54)=297\ mm^2$