Question

Find the center and the radius of the circle with the equation: x^2-2x+y^2+4y+1=0?

Answer 1

Center (h,k) is (1,-2) and radius r = 2

Explanation:

We need to find the center and radius of the circle of the given equation:

`x^2-2x+y^2+4y+1=0`

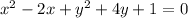
We need to transform the above equation into standard form of circle

`(x-h)^2 + (y-k)^2 = r^2`

where(h,k) is the center of circle and r is radius of circle.

Solving the given equation:

`x^2-2x+y^2+4y+1=0`

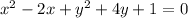
Moving 1 to right side

`x^2-2x+y^2+4y=-1`

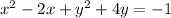
Now making perfect square of x^2-2x and y^2+4y

Adding +1 and +4 on both sides of the equation

`x^2-2x+1+y^2+4y+4=-1+1+4`

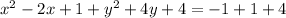
Now, x^2-2x+1 is equal to (x-1)^2 and y^2+4y+2 =(y+2)^2

`(x-1)^2+(y+2)^2=4`

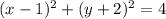
Comparing with standard equation of circle:

`(x-h)^2 + (y-k)^2 = r^2`

h = 1 , k =-2 and r =2 because r^2 =4 then r=2

So, center (h,k) is (1,-2) and radius r = 2