Question

Let f(x) = 1/x^2 (a) Use the definition of the derivatve to find f'(x). (b) Find the equation of the tangent line at x=2

Answer 1

(a)
`f'(x)=-(2)/(x^3)`

(b)
`y=-0.25x+0.75`

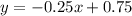
Explanation:

The given function is

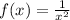`f(x)=(1)/(x^2)` .... (1)

According to the first principle of the derivative,

`f'(x)=lim_(h\rightarrow 0)(f(x+h)-f(x))/(h)`

`f'(x)=lim_(h\rightarrow 0)((1)/((x+h)^2)-(1)/(x^2))/(h)`

`f'(x)=lim_(h\rightarrow 0)((x^2-(x+h)^2)/(x^2(x+h)^2))/(h)`

`f'(x)=lim_(h\rightarrow 0)(x^2-x^2-2xh-h^2)/(hx^2(x+h)^2)`

`f'(x)=lim_(h\rightarrow 0)(-2xh-h^2)/(hx^2(x+h)^2)`

`f'(x)=lim_(h\rightarrow 0)(-h(2x+h))/(hx^2(x+h)^2)`

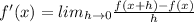
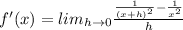
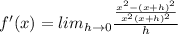
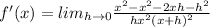
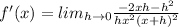
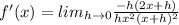
Cancel out common factors.

`f'(x)=lim_(h\rightarrow 0)(-(2x+h))/(x^2(x+h)^2)`

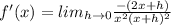
By applying limit, we get

`f'(x)=(-(2x+0))/(x^2(x+0)^2)`

`f'(x)=(-2x))/(x^4)`

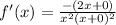
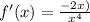
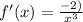`f'(x)=(-2))/(x^3)` .... (2)

Therefore
`f'(x)=-(2)/(x^3)`.

(b)

Put x=2, to find the y-coordinate of point of tangency.

`f(x)=(1)/(2^2)=(1)/(4)=0.25`

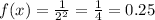
The coordinates of point of tangency are (2,0.25).

The slope of tangent at x=2 is

`m=((dy)/(dx))_(x=2)=f'(x)_(x=2)`

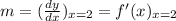
Substitute x=2 in equation 2.

`f'(2)=(-2)/((2)^3)=(-2)/(8)=(-1)/(4)=-0.25`

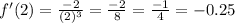
The slope of the tangent line at x=2 is -0.25.

The slope of tangent is -0.25 and the tangent passes through the point (2,0.25).

Using point slope form the equation of tangent is

`y-y_1=m(x-x_1)`

`y-0.25=-0.25(x-2)`

`y-0.25=-0.25x+0.5`

`y=-0.25x+0.5+0.25`

`y=-0.25x+0.75`

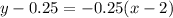
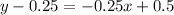
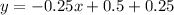
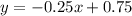
Therefore the equation of the tangent line at x=2 is y=-0.25x+0.75.