Question

What is the equation of the parabola with focus (-1,-1) and directrix y=1?

Answer 1

B

Explanation:

Given focus as (h,k) and directrix as y = mx + b, the equation of a parabola is given as:

`((y - mx - b)^2)/(m^2 +1)=(x - h)^2 + (y - k)^2`

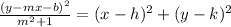
Hence, from the given focus & directrix, we have:

h = -1

k = -1

m = 0

b = 1

We can plug them into the formula and arrange to get:

`((y - mx - b)^2)/(m^2 +1)=(x - h)^2 + (y - k)^2\\((y - (0)x - 1)^2)/(0^2 +1)=(x - (-1))^2 + (y - (-1))^2\\((y-1)^2)/(1)=(x+1)^2+(y+1)^2\\y^2-2y+1=x^2+2x+1+y^2+2y+1\\-2y-2y=x^2+2x+1\\-4y=x^2+2x+1\\y=-(1)/(4)x^2-(1)/(2)x-(1)/(4)`

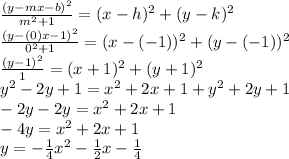
B is the correct answer.