Question

A. 8pi

B. pi

C. 2pi

D. 4pi

Answer 1

The length of the arc AC is 2π ⇒ answer C

Explanation:

* Lets revise some facts in the circle

- The length of the arc is depends on the measure of the arc and the

radius of the circle

- The length of the arc is a part of the length of the circle

- The length of the circle is 2πr

- The rule of the length of the arc =
`(\alpha )/(360)*2\pi r`,

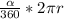where α is the measure of the arc

* Now lets solve the problem

- In circle P

∵ BC is a diameter

∵ BC = 24 ft

∵ The length of the radius of the circle is 1/2 the length of the diameter

∴ The length of the radius = 1/2 × 24 = 12 ft

- Ac is an arc in the circle

∵ The measure of the arc = 30°

∵ The length of the arc =
`(\alpha )/(360)*2\pi r` ,

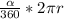where α is the measure of the arc

∴ α = 30°

∵ r = 12 ft

∴ The length of the arc =
`(30)/(360)*2(12)\pi=(1)/(12)*(24)\pi=2\pi`

∴ The length of the arc AC is 2π

Answer 2

Answer: Option C

`AC = 2\pi`

Explanation:

The arc length is calculated as

`L = \theta * R`

Then

`AC = \theta * R`

We know that

`BC = 24\ ft`

If BC is the diameter of the circumference then the radius R is:

`R = (BC)/(2)`

`R = (24)/(2)`

`R = 12\ ft`

Now we convert the anglo from degrees to radians
`\theta= 30\° * (\pi)/(180\°)\\\\\theta=(1)/(6)\pi`

Finally

`AC = (1)/(6)\pi * 12`

`AC = 2\pi`