Answer:
Part 1) The exact value of the arc length is
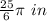
Part 2) The approximate value of the arc length is
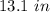
Explanation:
step 1
Find the circumference of the circle
The circumference of a circle is equal to
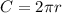
we have

substitute
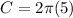
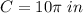
step 2
Find the exact value of the arc length by a central angle of 150 degrees
Remember that the circumference of a circle subtends a central angle of 360 degrees
by proportion

step 3
Find the approximate value of the arc length
To find the approximate value, assume
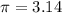
substitute
