Question

The base of pyramid A is a rectangle with a length of 10 meters and a width of 20 meters. The base of pyramid B is a square with 10-meter sides. The heights of the pyramids are the same. The volume of pyramid A is the volume of pyramid B. If the height of pyramid B increases to twice that of pyramid A, the new volume of pyramid B is the volume of pyramid A.

Answer 1

The volume of pyramid A is twice the volume of pyramid B. If the height of pyramid B increases to twice that of pyramid A, the new volume of pyramid B is equal to the volume of pyramid A.

Explanation:

Correct for plato :)

Answer 2

Part 1) The volume of pyramid A is two times the volume of pyramid B

Part 2) The new volume of pyramid B is equal to the volume of pyramid A

Explanation:

we know that

The volume of a pyramid is equal to

`V=(1)/(3)Bh`

where

B is the area of the base of pyramid

h is the height of the pyramid

Part 1

The heights of the pyramids are the same

Find the volume of pyramid A

Find the area of the base B

`B=10*20=200\ m^(2)`

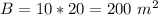
substitute

`VA=(1)/(3)(200)h`

`VA=(200)/(3)h\ m^(3)`

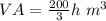
Find the volume of pyramid B

Find the area of the base B

`B=10^(2)=100\ m^(2)`

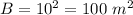
substitute

`VB=(1)/(3)(100)h`

`VB=(100)/(3)h\ m^(3)`

Compare the volumes

`VA=2VB`

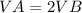
The volume of pyramid A is two times the volume of pyramid B

Part 2)

If the height of pyramid B increases to twice that of pyramid A

we have that

`VA=(200)/(3)h\ m^(3)`

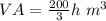
Find the new volume of pyramid B

we have

`B=100\ m^(2)`

`h=2h\ m`

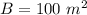
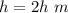
substitute

`VB=(1)/(3)(100)(2h)`

`VB=(200)/(3)h\ m^(3)`

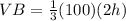
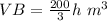
Compare the volumes

`VA=VB`

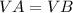
The new volume of pyramid B is equal to the volume of pyramid A