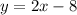Question

The equation of line AB is y = 2x + 4. Write an equation of a line parallel to line AB in slope-intercept form that contains point (3, −2). (4 points) y = 2x + 4 y = negative 1 over 2 x − 1 over 2 y = − 1 over 2 x − 7 over 2 y = 2x − 8

Answer 1

`y = 2x - 8`

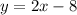
Step-by-step explanation

To find the equation of a straight line, we need the slope and a point on that line.

We were given the equation of another line that will help us determine the slope . The given line has equation:

`y = 2x + 4`

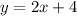
This equation is of the form

`y = mx + b`

where

`m = 2 \: \: is \: the \: \: slope.`

Since our line of interest is parallel to this line, their slopes are the same.

The line also contains the point (3,-2).

So we substitute the slope and point into the slope-intercept formula:

`- 2= 2(3)+ b`

`- 2 =6 + b`

`\implies \: b = - 2 - 6 = - 8`

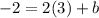
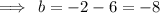
The required equation is

`y = 2x - 8`