Question

Determine the linear equation from the graph below.

1 Height of a balloon
3
+
.
.
.
.
.
Height (1000 ft)
10 20 30 40 50 60
Time (sec)

Answer 1

The equation of the given line is :y = 0.04x + 0.6.

Explanation:

From the given data , we can select two coordinates to determine the equation of the given line:

Let the point be
`(10,1),(60,3)`

The equation of the line will be determined by the help of point slope form:

Slope of the line =
`m=(y_2-y_1)/(x_2-x_1)`

`(y-y_1)=m(x-x_1)`

The equation of the line is :

`m=(3-1)/(60-10)=(2)/(50)=0.04`

`(y-1)=0.04(x-10)`

`y-1=0.04x-0.4`

`y=0.04x+0.6`

The equation of the given line is :y = 0.04x + 0.6.

Answer 2

Answer:
`y=(1)/(30)x+1`

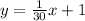
Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

The slope of the line can be calculated with this formula:

`m=(y_2-y_1)/(x_2-x_1)`

Pick to points of the given line. You can choose the point (60,3) and the point (30,2).

Then, substituting into the formula, you get:

`m=(2-3)/(30-60)=(1)/(30)`

You can observe in the graph that the line intercepts the y-axis at the point (0,1), therefore "b" is:

`b=1`

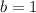
Substituting the slope and the y-intercept found into
`y=mx+b`, you get the equation of this line:

`y=(1)/(30)x+1`

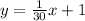
Where "y" represents the Height (1,000 ft) and "x" represents the Time in seconds.