Question

Which equation is the inverse of 2(x - 2)^3=8(7+y)​

Answer 1

`\large\boxed{y=2\pm√(28+4x)}`

Explanation:

`2(x-2)^2=8(7+y)\\\\\text{exchange x to y, and vice versa:}\\\\2(y-2)^2=8(7+x)\\\\\text{solve for y:}\\\\2(y-2)^2=(8)(7)+(8)(x)\\\\2(y-2)^2=56+8x\qquad\text{divide both sides by 2}\\\\(y-2)^2=28+4x\iff y-2=\pm√(28+4x)\qquad\text{add 2 to both sides}\\\\y=2\pm√(28+4x)`

Answer 2

y is inverse: 2 ±
`√(28+ 4x)` .

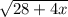Explanation:

Given: 2(x - 2)²=8(7+y)​.

To find: Find inverse.

Solution : We have given

2(x - 2)²=8(7+y)​.

Step 1: inter change the x and y.

2(y - 2)²=8(7+x)​.

Step 2:

Solve for y

On dividing both sides by 2

(y - 2)² = 4 (7+x)​.

Distributes 4 over ( 7 + x)

(y - 2)² = 28 + 4x

Taking square root both sides.

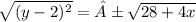`\sqrt{(y-2)^(2) } = ±√(28+ 4x)`.

y - 2 = ±
`√(28+ 4x)`.

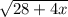On adding both sides by 2

y = + 2 ±
`√(28+ 4x)` .

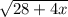Therefore, y is inverse : 2 ±
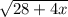`√(28+ 4x)`.