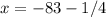Question

Write the equation in vertex form and then find the vertex, focus, and directrix of a parabola with equation x=y^2+18y-2

Answer 1

Part 1) The vertex is the point (-83,-9)

Part 2) The focus is the point (-82.75,-9)

Part 3) The directrix is
`x=-83.25`

Explanation:

step 1

Find the vertex

we know that

The equation of a horizontal parabola in the standard form is equal to

`(y - k)^(2)=4p(x - h)`

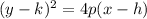
where

p≠ 0.

(h,k) is the vertex

(h + p, k) is the focus

x=h-p is the directrix

In this problem we have

`x=y^(2) +18y-2`

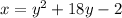
Convert to standard form

`x+2=y^(2) +18y`

`x+2+81=y^(2) +18y+81`

`x+83=(y+9)^(2)`

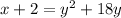
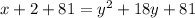
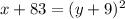
so

This is a horizontal parabola open to the right

(h,k) is the point (-83,-9)

so

The vertex is the point (-83,-9)

step 2

we have

`x+83=(y+9)^(2)`

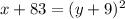
Find the value of p

`4p=1`

`p=1/4`

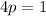
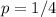
Find the focus

(h + p, k) is the focus

substitute

(-83+1/4,-9)

The focus is the point (-82.75,-9)

step 3

Find the directrix

The directrix of a horizontal parabola is

`x=h-p`

substitute

`x=-83-1/4`

`x=-83.25`